• 作者：Gordon Reid
  
• 编译：Rejor（@Evilsine）
  
• 出处：Sound On Sound

在本系列的前三篇文章中，我们介绍了震荡器、包络发生器、VCA 以及 LFO 等合成器模块的功能、它们的工作原理以及它们在减法合成器中扮演的角色。现在，我们终于要讲到减法合成的核心——滤波器（filters）了。但如果你觉得我会讲「把共振（resonance ）调到 11，然后用 24dB/octave VCF 扫频，就能得到经典的模拟音色」这类只知其然的东西，这篇文章恐怕会让你失望了。

要想知道为什么有些滤波器听感悦耳，另一些听起来却并不尽如人意，你就需要深入了解滤波器的工作原理。很不幸，滤波器是所有合成器中最常被误解的模块。常见的误区是：滤波器的作用就只是将信号的一部分削弱。实际上，无论是模拟还是数字世界，滤波器的功能可远远不止减弱信号这么简单。 

为了能够明确看到音频信号在被滤波器处理的过程中到底放生了什么，你需要先理解一些相位关系的基础知识。让我们再往回看，从本系列第一篇文章中引入的正弦波开始说起。 

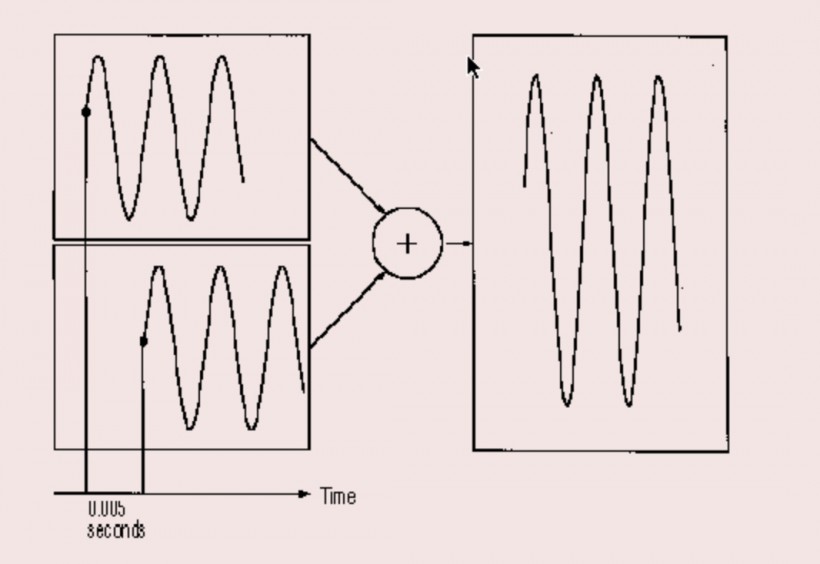
首先，想象如果你使用混音器将两个正弦波混合起来会发生什么。你可能已经猜到了：两个一致的波形相加得到的还是相同的波形，不过响度会更高（如图 1）。

但如果你等到上面的波形进行到其周期一半的时候再引入下面的波形呢？图 2 中展示了这一情况，如果你讲这样的两个波形相加，它们会彼此抵消，因此你将听不到任何声音。也就是说，尽管这两个波形单独听是完全一致的，但将其混合却得到的是无声。

这一结果十分重要，通过该规律我们可以知道，只需要频率与响度两个参数就可以定义一个单一的正弦波，但如果要将两个正弦波混合在一起，你还需要考虑两个波形之间的偏移有多少。这样的偏移通常被称为一个波形与另一波形之间的「相位（phase）」。相位以度数来计量，和量角器上的度数一样（如果你想知道为什么要用度数来表示相位的话，你可以阅读本文末尾的「相位的度数表示」拓展部分，但如果你不想再考虑枯燥的数学知识了，可以直接继续阅读下面的文章）。 

当然，你可以将两个偏移量（即相位差）任意的任何两个正弦波混合在一起，混合后的波形的响度会处于图 1 中的两倍响度以及图 2 中的 0 响度之间（但如果你将两路信号通过立体声而不是单声道的方式混合，你将得到一个十分不同的效果。但这是改天的话题了，这篇文章中暂时不予讨论）。 

让我们以时间差的角度来看待相位差。假如说你有一个 100Hz 的正弦波，也就是说每秒钟震荡 100 个周期，因此，每完成一个周期所需的时间为 0.01 秒。对于该信号来说，半个周期的偏移（如果你已经阅读了文末的拓展知识，你会知道半个周期的偏移等于 180 度的相位差，但如果你还没读，也不用担心）为 0.005 秒，即 5 毫秒。图 3 可以帮助你理解这一过程。

现在想象两个频率为 200Hz 的正弦波，对于 200Hz 的波形来说，5 毫秒的时间可以完成一整个周期。如图 4，如果使其中一个正弦波偏移 5 毫秒，另一个正弦波已经完成了一整个周期，这时这两个正弦波又回到了同相的状态，如果将这样的两个正弦波相加，得到的会是一个响度为原波形两倍的正弦波。

让我们深吸一口气，然后想想看如果把这一概念应用于更为复杂的波形中会发生什么。以锯齿波为例，你可能还记得我们在本系列的第一篇文章中介绍了锯齿波的每一个谐波均存在，所以如果一个锯齿波的基频（即第一谐波）为 100Hz，那么其第二谐波的频率就为 200Hz，第三谐波为 300Hz...以此类推。如果将同样频率，但彼此偏移半个周期的两个锯齿波相加，基频会被抵消；但位于 200Hz 的第二谐波的响度会翻倍；三倍基频的第三谐波会被抵消，但第四谐波响度翻倍，第五谐波被抵消...以此类推。这样我们得到的将是一个谐波位于 200Hz、400Hz、600Hz...等等的波形。实际上，这一波形就是一个响度与原始波形一致，但频率为原始波形两倍的锯齿波。 

这一有悖直觉的结果就是我们今天的第一条结论： 

将「失相」的信号混合在一起并不一定会将其两者抵消。事实上在真实世界里完全抵消的情况几乎根本不会发生。  

但这还只是相位偏移的几种最简单的情况之一。想想看如果将这一规律运用于真实世界中的复杂波形上会发生什么：部分谐波的幅度会减小，另一部分谐波的幅度会增加，还有一些部分的谐波会被完全抵消，剩下一部分的谐波会完全重叠从而幅度翻倍。傅里叶分析告诉我们任何复杂波形——无论是人的说话声还是乐器的声音都可以被看作是由无数个正弦波组成的频谱构成的。所以说，假设对于只有相位有一定偏移，其他方面完全相同的两个波形来说，构成这两个波形的每个谐波之间也会有不同幅度的相位偏移。如果在频谱分析仪上观察这一结果的话，你会看到一个类似于横放的梳子的图案，「梳齿」之间的距离（即被抵消的谐波）由时间差决定（见图 5）。

换句话说，当你将除了相位偏移之外其他方面完全相同的两个波形混合在一起时，两个波形的谐波之间的相位差导致了滤波。因为这种滤波的形状与梳子十分形似，所以使用这一技术的滤波器被称为梳状滤波器（Comb Filter）。梳状滤波器在合成器中被广泛运用，从经典的模拟模块化合成器 Analogue Systems RS Integrator 到基于 DSP 的 Waldorf Q 上都可以找得到到梳状合成器的身影。 

了解了关于相位的的知识之后，不难看到相位与音频滤波之间的密切关联。但想想看，如果相位变化可以导致滤波，那么滤波能否导致相位变化呢？答案是：当然可以。

观察图 6 中的电路图，这一电路非常简单，只使用了两个电子元器件：一个电阻器与一个电容器，不过这一简单电路构成一个完全可用的滤波器，叫做 RC 低通滤波器。任何新手合成器用户都知道，低通滤波器允许低于「截止频率」的所有谐波通过，所有高于截止频率的谐波则会被削减。对于这一简单的滤波器来说，它的截止频率取决于其元器件的参数，截止频率以上的信号被削减的速率则由电路的构造决定。 

我们暂时不考虑信号被削减的速率，这一话题将留给下一篇文章探讨。本文我们将专注于这一滤波器会对被输入进去的信号相位造成什么样的影响。

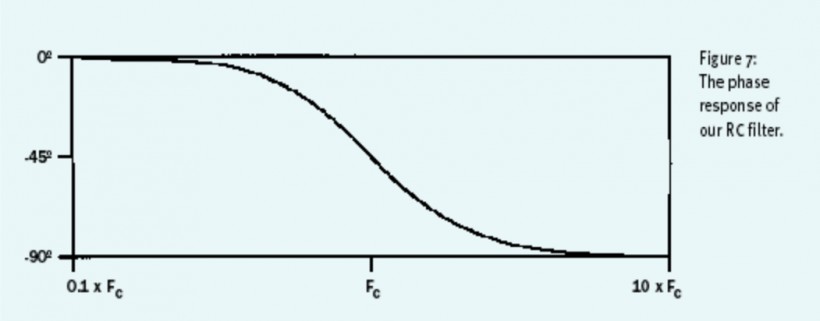
观察图 7，该图是上文的简单 LPF 的「相位响应（phase response）」属性。该图展示了任意被输入进滤波器中的频率及其相位将被偏移的程度。不难看到，该滤波器几乎没有对低频信号的相位产生大幅影响，然而信号频率越高的位置，其相位被偏移得就越大。位于截止频率的信号被偏移了八分之一周期（-45 度），信号最高频的位置则被整整偏移了 -90 度。 

由于这些概念有些难懂，让我们以 100Hz 的方波为例，看看这一 RC 滤波器在实际的模拟合成器中到底起什么样的作用。 

正如我们在本系列的第一篇文章中介绍的：任何传统波形都可以被分解成一些列谐波，这些谐波被称为基础频率及其泛音。这一例子中，我们的输入信号（方波）的基础频率为 100Hz，其第二谐波（200Hz）不存在，但拥有位于 300Hz 的第三谐波，并且第三谐波的幅度为基频幅度的三分之一。接着，第四谐波不存在，幅度五分之一的第五谐波位于 500Hz 的位置，以此类推...当其所有谐波均同相的情况下，该波形如图 8 所示。

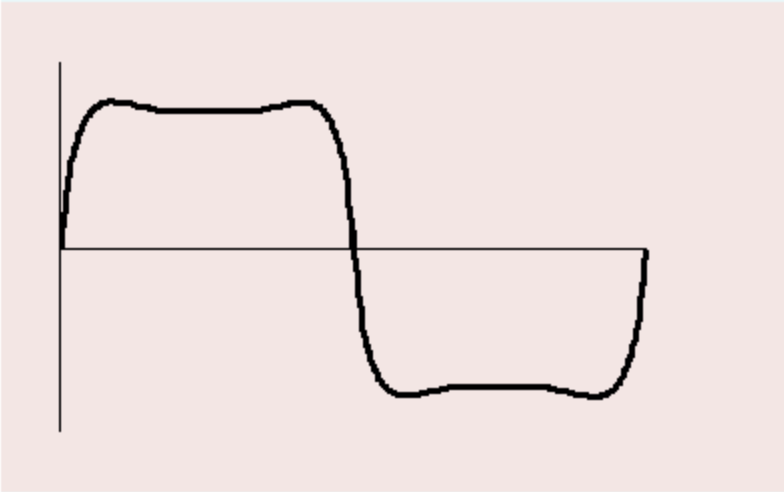
现在，假设我们的简易 RC 滤波器拥有 400Hz 的截止频率，并且该滤波器截止频率一下的相位响应均为 0。这种情况下的结果应该不难想象：波形的基频与第一泛音（100Hz 与 300Hz）将不会被减弱，但所有高于 500 Hz 的泛音均会根据相位响应发生相应幅度的衰减。经过这一处理之后的波形（可能会和你的预料有些不同）如图 9 所示。

现在再让我们把滤波过程中每个谐波产生的相位偏移考虑进来，我们现在得到的将会是一个形状十分不同的波形。可以看到，经过滤波之后的真实波形与原始方波比起来产生了明显的失真（如图 10）。

由此我们可以得到本文最重要的规律： 

滤波器不光只是使波形的谐波产生衰减，它还可以通过改变谐波的相位偏移从而使得波形失真变形。 

不过由于本文列举的方波与滤波器非常简单，尽管可以看到经过滤波的图 9 与图 10 中的波形与原始波形的区别，你可能并不能听出滤波造成明显的差异。但还是那句话，真实世界中的声音要比简单的方波等波形复杂得多，滤波可以对许多真实声音造成巨大的改变。当然，滤波器的种类也远不是只有本文中列举的简易 RC 低通滤波器一种，如果使用的是 Moog 滤波器的话，滤波产生的效果又会与上文大相径庭...不过我们暂时先把这些留给以后的文章。 

拓展知识：为什么相位偏移可以用度数表示 

数学中的度数不是用来描述角度的大小与旋转的幅度的吗？这要取决于你如何看待这一问题。想象一个正弦波波形，如下图中的 (c)。在某一时刻，该波形从零点开始上升，运动到其周期 1/4 的时刻到达顶峰，到周期一般的位置重归零点，运动至 3/4 周期的时候跌至最低，然后在周期最末尾重归零点，往复循环进行。 

然而正弦波的波形可以用另一种方式描述。想象一个圆盘以一个固定的速度旋转，如上图中的 (a)，如果只考虑圆周上的任意一个点的纵向运动轨迹，你得到的将是上图中 (b) 这样的上下往返移动。但想象将这一上下移动轨迹画在一张纸上，但在同时以固定的速度横向移动这张纸，你得到的也将会是上图中 (c) 的正弦波，如下图所示： 

通过这一思路我们可以使用度数这一个单位同时表示圆周旋转的幅度与正弦波的周期。正弦波由 0 度开始，到达最高点时位于 90 度，进行至 180 度时降回 0，到达最低点时位于 270 度，与 360 度的时候完成一整个周期，与 0 度重叠。

这是一种表示波形属性的巧妙方式，并且可以非常简单地描述相对相位。比如说，如果两个正弦波彼此相位偏移半个周期，那么你就可以说这两个波形处于「180 度失相关系（因为当一个波形位于 180 度的时候另一个波形位于 0 度的位置）」。

---

点此查看全部正在连载中的《揭秘合成器》系列教程。