揭秘合成器(11):振幅调制
- 作者:Gordon Reid
- 编译:Rejor(@Evilsine)
- 出处:Sound On Sound
如果调制的信号源是一个音频频率范围的振荡器,而且调制对象为音频信号流中的 VCA 增益,那么我们管这样的调制叫做振幅调制(Amplitude Modulation),或者简写成 AM。振幅调制在我看来是一个非常有趣的话题,其中的一个原因是 AM 可以造成十分出人意料的效果:AM 造成的并不是极其迅速的颤音,而是原始信号中并不存在的谐波频率!但这一现象是怎样产生的呢?
振幅调制的原理其实十分反直觉,所以我们要使用数学才能对它进行理解。尽管 AM 背后的数学原理并非极其复杂,但如果你想跳过本文的下一部分直接阅读本文后半的实际运用也完全没有问题。如果你想尝试理解 AM 的数学原理,不妨继续阅读,或许你也会觉得它其实蛮有意思…
A₁=a₁cos(w₁t)
算式 1: 一个简单的余弦波
利用算式 1 我们可以求得一个余弦波频率(w)在任意瞬时(t)的振幅(即任意时刻时波形的幅度,A)。当然,我们完全可以使用正弦波取代这里的余弦波,毕竟两者的波形完全一致,它们唯一的区别在于相位,但这里我之所以使用余弦波是因为这样可以些许简化我们需要的数学运算。上述算式中还有另外一个变量,小写 a 用来代表波形振幅的峰值(波形一个周期内幅度的最大值)。
你或许注意到了算式 1 中的每个变量(时间 t 除外)的右下方都有一个「1」的角标,这一角标是用来将下文中的算式与我们的第一个波形区别开来的。
A₂=a₂cos(w₂t)
算式 2: 另外一个余弦波
观察算式 2,不难发现算式 2 和算式 1 完全一致,唯一的区别在于变量的角标为 2,而不是 1。这说明我们有另外一个波形需要考虑,并且这一波型拥有与算式 1 不同的最高振幅以及振荡频率。
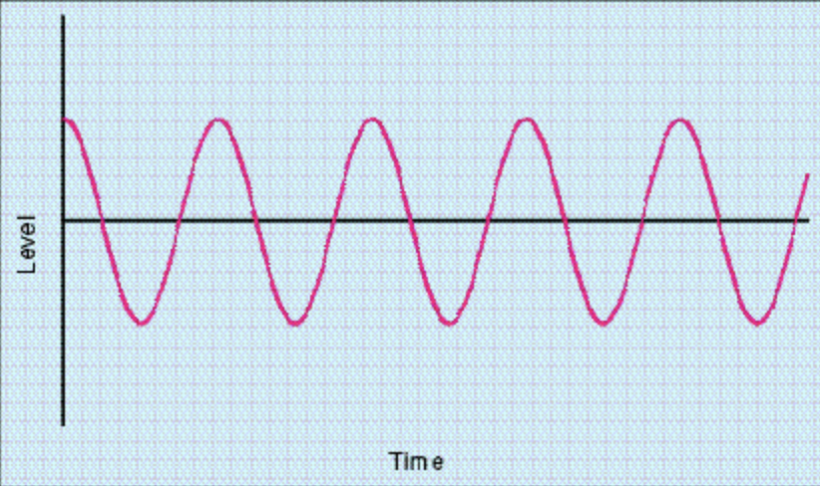
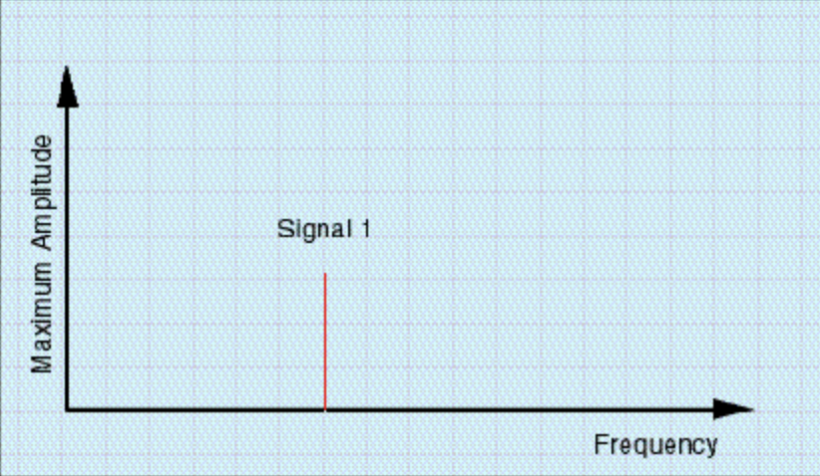
让我们假设信号 1 的振幅 a₁ 为信号 2 振幅 a₂ 的二分之一。让我们将两个信号的振幅分别叫做增益 1 和增益 2。现在让我们假设波型 1 的频率 w₁ 是波型 2 频率 w₂ 的 1.5 倍,比方说信号 1 的频率为 300Hz,信号 2 的频率为 200Hz。这两个信号的波形分别为图 1 和图 3,它们的频谱构成分别为图 2 和图 4。虽然上面的两个算式看上去或许晦涩难懂,但大多数人对于图 1 和图 3 的波形都多多少少有所熟悉,其实上面的算式和波形图表示的是完全一致的信息。
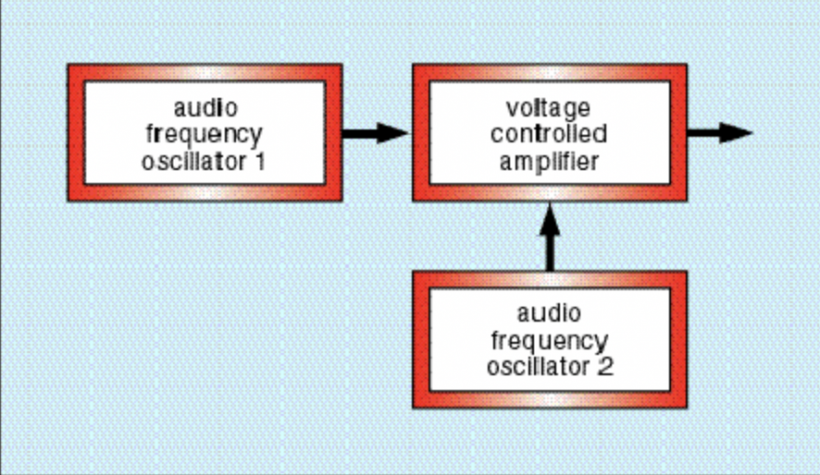
现在让我们想象一下如果将上面的两个信号混合起来会发生什么。图 5 展示的是混合音频信号的合成器流程图,图 6 则是经过混合的复合信号(这一复合信号任意时刻的振幅均为两条原始信号同样时刻的两波形振幅之和),图 7 是这一信号的谐波构成。
这一结果并非十分有趣。但让我们对上面的合成器流程进行些许改变,将信号链中的混音器用压控放大器,即 VCA 代替。接着让我们把信号 1 输送至 VCA 的音频输入中,不过这次让我们使用信号 2 调制该 VCA 的增益参数,就像我们在上一篇文章中使用 LFO 一样。因此,信号 2 成为这一流程中的调制器(Modulator),而信号 1 则为载波器(Carrier),见图 8。
别忘了,算式 1 中变量 a₁ 代表的是波形的最大振幅,为了便于理解,让我们假设这一振幅等于 VCA 的增益。但因为我们现在使用第二条信号的瞬时振幅来对原始信号进行调制,所以当调制器信号的波形为正值(即其电压高于 0V 轴)时,VCA 的增益将随之上升,当调制器波形为负值时,VCA 的增益将随之减弱。但调制器信号在任意时刻的振幅 A₂ 我们都可以使用算式 2 进行计算。
所以我们现在可以得到一条新的算式,该算式输出信号的振幅为 a₁ 与 A₂ 只和:
A₁=(a₁ + A₂)cos(w₁t)
算式 3: 决定输出信号波形的算式
我们可以将算式 2 中 A₂ 的求法代入至算式 3,从而得到算式 4,然后将其展开得到算式 5:
A₁=(a₁ + a₂cos(w₂t))cos(w₁t)
算式 4: 将 A₂ 代入至算式 3
A₁=a₁cos(w₁t) + a₂cos(w₂t)cos(w₁t)
算式 5: 将算式 4 展开的结果
算式 5 看上去或许要比算式 3 复杂,但两者描述的信号与 VCA 关系其实完全一致。观察算式 5 的右半边,你会发现它包含两个余弦函数的乘积。余弦函数的乘积很难进行直观理解,不过幸运的是利用一条数学原理,我们可以将频率为 X 和 Y 的两条余弦函数的乘积分离成 cos(X+Y) 和 cos(X-Y) 两项。如果你不理解上面这一部分,别担心,你只需要记住我们可以将算式 5 中的右边一项分离成算式 6 中的两项,其中一项是频率为 w₁ + w₂ 的波形,另一项是频率为 w₁ - w₂ 的波形。
A₁=a₁cos(w₁t) + 1/2(a₂cos(w₁ + w₂)t) + 1/2(a₂cos(w₁ - w₂)t)
算式 6: 振幅调制的结果
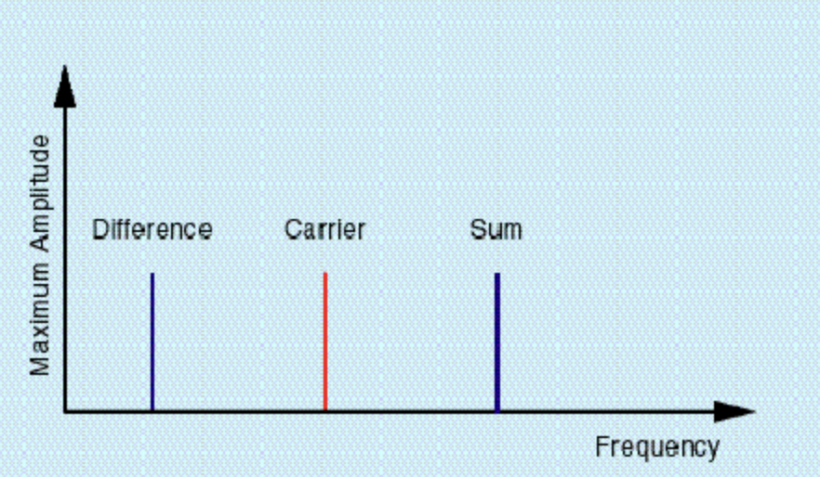
仔细观察算式 6,你会发现该算式的第一项与算式 1 中的原始余弦波,即载波器信号完全一致。现在请思考一下算式 6 第二项中的 w₁ + w₂ 的意义。这一定代表的是频率为载波器与调制器频率只和的波形。同样的,第三项代表的是频率为载波器与调制器频率之差的波形。换句话说,振幅调制不光保留了原始的载波器信号,还制造了分别叫做和(Sum)与差(Difference)的两条全新信号。
图 9 展示的是算式 6 代表的波形。可以看到这一波形要比图 6 中简单地将两条信号混合起来制造的波形复杂得多。
图 10 为图 9 波形的频谱,注意调制器的原始频率完全消失,生成的和差信号分别具备调制器原始振幅的二分之一(算式 6 中的 1/2 也说明了这一点)。
介绍了这么多振幅调制的理论,让我们讨论一下怎样可以将 AM 技术实际运用至合成器中。要想回答这一问题,我们需要考虑振幅调制的两种情况:第一是调制器频率保持恒定时的情况,另外一个是调制器和载波器两者的频率均由键盘(或者其他任何控制电压)控制时的情况。
让我们先来思考一下使用键盘演奏载波器信号,而调制器信号(恒定振幅)的频率保持不变(比如说 100 Hz)时的情况。
例 1
当载波器频率同样为 100 Hz 时,振幅调制造成的三个频率分别为:原始的 100Hz,100 - 100 = 0Hz,以及 100 + 100 = 200Hz。它们分别为载波器的原始信号、振幅调制的差信号以及和信号。或许你会认为频率为 0Hz 的信号并不具备任何影响,然而事实并非如此。这一频率仍然具备(调制器信号二分之一的)振幅,因此可以导致输出信号的偏移。我们将这一现象称作 DC 偏移(direct current offset,直流偏移),因为位于 0Hz 的信号不具备振荡频率。观察图 11,可以看到输出信号的一大部分位于 0V 线之上,这一现象就是 DC 偏移导致的。当信号被合成器的其他模组,例如滤波器和放大器进行处理时, DC 偏移可能会造成明显的影响。但本文我们并不会对此进行深入探讨。

图 11: 载波器振幅 a₁ = 1,频率 w₁ = 100Hz,调制器振幅 a₂ = 1,频率 w₂ = 100Hz 的振幅调制
振幅调制后的另外两条信号分别为位于 100Hz 的载波器原始信号和位于 200Hz 的和信号。当然,这里的和信号频率正好是载波器原始频率的两倍,也就是说它比载波频率正好高一个八度,因此这一结果听上去会十分谐和,或者「悦耳」。我们可以将输出的三条频率分别概括为载波器频率的百分之 0、百分之 100 和百分之 200。
例 2
假设我们将音符从键盘上移高一点,比如说现在的载波器频率为 200Hz。因为调制器的频率保持 100Hz 不变,所以振幅调制造成的三个频率分别为载波器原始的 200Hz、载波与调制信号的频率差 100Hz 以及频率和 300Hz。该振幅调制的结果多多少少仍然谐和,因为差信号正好位于载波器信号的一个八度之下。然而和信号与载波器并不具备谐和关系。尽管如此,这一情况也还是一个特例,因为和信号为差信号的第三谐波,因此最终的输出信号仍然具备一定的「音乐性」,尽管载波器(差信号的第二谐波)是主导频率。我们可以将该情况的三条频率概括为载波器频率的百分之 50、百分之 100 和百分之 150。
例 3
现在让我们为载波器选择一个较为随机的频率。比如说如果我们的载波器频率为 371Hz 时将会得到什么样的结果呢?这时的和差信号分别为 271Hz 和 471Hz,它们之间不存在谐和关系。输出波形的三个频率分别大致位于载波信号的百分之 73、百分之 100 和百分之 127 的位置。因此我们将最终得到一个不和谐的声音。
实际上,当调制频率保持不变时,振幅调制制作的大多数音色都将会是类似上面的不谐和声音。类似例 1 和例 2 的特例其实十分罕见。因此固定调制器的 AM 合成最适合用来制作演奏不同琴键时变化巨大的激进、非常规的音效。你可以通过提升或降低调制器的振幅从而控制音色不谐和的程度。
例 4
让我们回到例 2,载波器仍具备 200Hz 的频率,调制器频率为 100Hz。和之前一样,输出信号仍将包含原始的 200Hz,以及和差信号的 300Hz 和 100Hz。不过这次我们会对合成器的流程进行些许改变,使得当你使用键盘演奏载波器时,调制器的频率也会随之改变。比如说,如果你演奏一个频率为 400Hz 的载波信号(原始 200Hz 的一个八度之上)调制器的频率也将随之翻倍,和差信号因此将分别变成 600Hz 和 200Hz。不管演奏什么样的音符,差、载波与和信号的频率将总是保持百分之 50、百分之 100 和百分之 150 的比率。尽管最终的输出信号频率翻倍,其波形将保持不变,因此我们可以得到一个恒定不变的音色。这类振幅调制可以帮助我们制作可以使用键盘正常演奏的拥有复杂谐波构成的音色。
总而言之:振幅调制可以帮助我们制作和演奏仅仅使用传统振荡器难以得到的复杂音色。
当然,直到这里我们所讨论的还仅仅只是简单的正弦波的振幅调制。你当然还可以使用其他类型的波形进行振幅调制。如果调制器和载波器分别具有一个基础频率和一个额外的谐波,那么使用振幅调制,我们得到的将不仅仅是一条差信号和一条和信号总共两条新信号,而是八条全新的谐波。如果调制和载波频率分别具备三条谐波,那么振幅调制将生成 18 条额外的谐波。如果它们分别具备四条谐波,生成的谐波将上升至 32 条,以此类推…
我们完全可以使用拥有复杂谐波构成的波形,比如说方波或锯齿波等波形进行振幅调制。这些复杂波形的振幅调制和简单的正弦波振幅调制原理完全相同,不过为了理解它们我们需要进行许多次计算。
或许你还记得锯齿波具有基础频率的所有整数倍谐波。比如说,一个基础频率为 100Hz 的锯齿波频谱由 100Hz, 200Hz, 300Hz, 400Hz 等等整数倍谐波构成。75Hz 的锯齿波频谱中包含的频率则为:75Hz, 150Hz, 225Hz…以此类推。所以如果用一个频率为 75Hz 的调制器对 100Hz 的载波信号进行振幅调制将会得到怎么样的结果呢?
不难想象载波信号的基频将与调制器的基频进行交互,产生频率为 25Hz, 100Hz, 与 175Hz 的三条谐波。它同时也会和调制器的第二谐波进行相互作用,产生 -50Hz, 100Hz, 以及 250Hz 的另外三条谐波(你或许在想 -50Hz 的频率是什么样的,其实负数频率和正频率听起来完全相同,也就是说你将简单地听到 50Hz 的声音)。接着是调制器的第三谐波(造成 125Hz, 100Hz 和 325Hz谐波)、第四谐波、第五和第六等等等等…天呐,好复杂!
但这还不算完,别忘了载波器的第二谐波也会与调制器的所有谐波频率产生交互,接着是载波器的第三谐波、第四谐波、第五谐波…等等等等。幸运的是,锯齿波等波形除了前几个谐波之外的其他谐波频率振幅都十分微小,因此在实际的运用中你可以多少忽视复杂波形的高次谐波。即便如此,不难想象对这些复杂波形进行振幅调制将会得到十分复杂的音色。振幅调制得到的波形可以作为使用滤波器和其他调制器进行复杂音色合成时十分不错的起点。
上面的所有例子中我们都假设你的合成器中的 VCA 完美运作,并且没有任何调制信号泄漏至最终的输出信号中。然而根据我的经验,事实完全并非如此,不过极其高品质的 VCA 可以保证信号泄漏处于合理的水平。尽管如此,即使仅仅只有一小部分调制信号泄漏至输出信号也会明显增添最终音色的不谐和感。
不过,还有另一种合成器模块可以(在理想情况下)将调制器和载波器的信号一同从输出信号中除去。这类模块叫做环形调制器(Ring Modulator,RM),虽说环形调制听上去很神秘,其实它只是振幅调制的一种特殊情况。另外,环形调制只有在调制信号和载波信号两者波形中心准确居于 0V 轴时才可以进行。为了实现这一点,许多环形调制器具备 AC 耦合(AC-couple)功能,也就是说(至少在理想情况下)输入信号中的任何 DC 偏移将会在进行调制之前被除去。环形调制得到的声音只含两条输入的和差信号,并不包含任何输入信号本身。还有一小部分环形调制器具备 DC 耦合功能,它们的运作方式和 AC 耦合 RM 有些许区别。其中最明显的区别在于它们允许将载波和调制的原始信号输送至最终输出的信号中。ARP 2600 等合成器中的 RM 调制器允许你在 AC 和 DC 耦合模式之间进行切换,以便制作两类不同的声音。
本文的最后,请思考一下如果我们使用信号 2 对低通滤波器的截止频率,而不是 VCA 的增益进行调制时将会发生什么呢?别担心,这一情况并不需要复杂的讨论和难以理解的数学原理。
想象一个复杂波形,它的其中一个谐波刚好位于滤波器截止频率 Fc 上方的某个位置。当你对 Fc 的频率进行调制时,你会发现有时该谐波的振幅会随着调制大幅度衰减,而另外一些时候衰减则并没有这么巨大。换句话说,该谐波其实相当于在被滤波器的行为变化而振幅调制。信号中的其他谐波也会根据调制的宽度(调制器的最大振幅 a₂)或多或少受到同样的影响。所以说这时,并不是一系列谐波在被另一系列谐波调制,我们只有一系列谐波,但其中的每一个单一谐波都以不同方式在被进行调制。
终于,对于振幅调制(即音频信号范围内的震音)和滤波器调制(即音频信号范围内的嗥音)的讨论到此为止就告一段落了。不过,既然我们可以用音频范围内的信号对 VCA 的增益和滤波器的截止频率进行调制,我们也一定可以使用音频信号对振荡器的振荡频率进行调制吧?没错,我们管这类调制叫做频率调制(Frequency Modulation,即 FM)。关于 FM 合成的深入探讨尽请期待本系列的下一篇文章。
文章出处 https://www.soundonsound.com/techniques/synth-secrets-all-63-parts-sound-on-sound
转载新闻请注明出自 Midifan.com
-
2022-05-06 10:18
 匿名
期待
匿名
期待 -
2022-03-25 18:28
 期待下一篇
期待下一篇